전공 수학을 공부하다 어느 수준이상이 되면, 정의를 받아들이는데에는 문제가 없다.
사실 그 정의를 그 순간 이해하고 외우는 것보다 중요한 것은
그러한 수학용어를 만든 배경과 쓰임을 알아야 한다. 그래야 안까먹고 중요함도 안다.
그러한 것들을 여기다가 적어보겠다.
대부분은 위상수학과 해석학 위주일 것이다. 대수학은 방학때나 적을 거임
1. First-Countable Space
Definition:
a space X is said to be first-countable if each point has a countable neighbourhood basis (local base).
That is, for each point x in X there exists a sequence U1, U2, … of open neighbourhoods of x such that for any open neighbourhood V of x there exists an integer i with Ui contained in V.
쓰임:
이것이 만족되어야, x in the closure of A <-> A상의 수열이 존재 s.t. cv to x. 가 성립한다.
(<-는 First countable아니어도 성립)
2. Separable Space
Definition:
a topological space is called separable if it contains a countable dense subset; that is, there exists a sequence 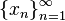 of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
쓰임:
f:X->Y, X:Separable, Y:Hausdorff, f:conti, 이때, X의 countable dense subset의 원소의 f값만 결정지어주면 f는 determined된다.
(즉, countable개만 정의해주면 나머진 지정됨)
3. Second-Countable space
Definition:
a topological space  is second countable if there exists some countable collection
is second countable if there exists some countable collection 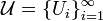 of open subsets of
of open subsets of  such that any open subset of
such that any open subset of  can be written as a union of elements of some subfamily of
can be written as a union of elements of some subfamily of 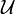 .
.
쓰임:
즉 관심가질 open sets의 개수를 countable개로 제한시켜버리는데 의의
4. Lindelof Space
Definition:
a Lindelöf space is a topological space in which every open cover has a countable subcover.
쓰임:
모든 open cover의 size를 줄인다.(Countable개만 생각해도 됨)
note)
각각의 용어들이, 용어 그 자체가 정의를 표현을 못하고 있다.
잘 외워야한다.
First-countable:각 점마다 countable basis가 존재
Second-countable:topology의 countable basis가 존재
Separable:X의 countable dense subset이 존재
Lindelof:open cover의 countable subcover가 존재.
5. T0, T1, T2, T2(1/2), T3, T4, T3*1/2
의미:
T0
Motive:X의 서로 다른 두 원소 a,b가 같은 neighborhood를 갖는다면, topologically indistinguishable
쓰임:X의 모든 원소가 topologically distinguishable임을 보장
T1
Motive:Finite set은 closed여야만 할 것 같다. Closed의 의미를 생각해본다면(limit에 닫혀있음에 따와서 closed라고 정의함)
쓰임:Finite Set은 closed임을 보장
T2
Motive:X의 서로 다른 두 원소 a,b가 open set에 의해 separated됨
쓰임:수열의 수렴값(point)가 존재한다면 유일
T2(1/2)
Motive:X의 서로 다른 두 원소 a,b가 closed set에 의해 separated됨, 1/2이 붙은 이유는 Hausdorff와 functionally Hausdorff사이에 있어서 1/2가 붙었다.
쓰임:
6. locally ~
(1) local Lp Space
Motive:1<=p<=inf 사이에서 Lp space는 포함관계가 없다. 그러나, local하게 생각하면(p norm을 잴 때의 영역을 finite하게 만들어버린다면)포함관계가 존재한다.
7. Vitali's Covering Lemma
내용:Bdd set E in R^n의 open cover(오직 ball로만 구성된)에 Lindelof적용하듯이, countable개만 꺼내와서 open cover하나 만듬
(꺼낼땐 disjoint하게 꺼내고, cover할땐 반지름을 3배해서)
의미:Lebesgue's Theorem에 적용(일반적인 미분을, 볼에서의 정적분에다가 극한을 씌우는 형태로 바꾸기때문에 ball형태가 중요)
8.
'제거된 것' 카테고리의 다른 글
| 2012/12/5 영어단어 (0) | 2012.12.05 |
|---|---|
| 인생 계획 (0) | 2012.12.05 |
| 2012/12/4 영어단어 (0) | 2012.12.04 |
| 2012/12/4 영어단어 (0) | 2012.12.04 |
| 아 (0) | 2012.12.03 |